Netduino Day 2: Interfacing a Character LCD
|
|
Liquid Crystal Displays (LCD) are a great choice of output device for displaying alphanumeric characters in real time. They are also very useful if your project requires an interactive user interface for data input. Besides, they are inexpensive, consume less power than LED displays, and give a more professional look to your project. Today we will explore how to interface an HD44780 based character LCD to Netduino to display alphanumeric characters. For technical details of the HD44780 driver, please read its datasheet as well as its interfacing example with chipKit.
Circuit Setup and Theory
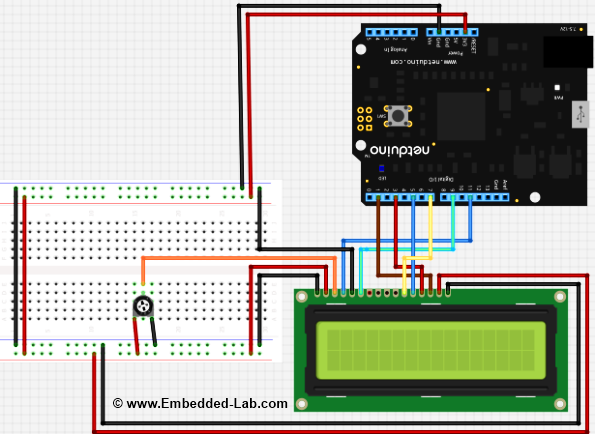
Connection wise it’s really simple. The LCD is operated in 4-bit mode, and therefore pins 7 through 10 (D0-D3) of the LCD are unused. The four most significant data bits, D4-D7 (pins 12 through 14), receives LCD data/command through Netduino I/O pins 7, 5, 3, and 1, respectively. Similarly, the Register Select (R/S) and Enable (E) signal lines of the LCD are driven by Netduino I/O pins 11 and 9, respectively. LCD pins 1, 2, 3, 4, 15 and 16 are related to power supply, contrast adjustment and backlight LED display, and are connected appropriately as shown below. To understand how LCD works, I have to point you to a different document as it is explained better over there. In Interfacing a Character LCD,Raj explains about the communication in 4 bit mode and he also talks about the basics of HD44780 LCD driver. For more technical details, see Hitachi HD44780U (LCD-II) datasheet.
Connection With Netduino / Netduino Plus
C#.NET Program
There are two ways we can look at the program, one in a very simple way and other, obviously, harder way. In simpler way we don’t worry about what’s inside the LCD class (or a library) rather use some of the exposed methods or properties. Let’s take a look at the simpler things first.
LCD lcd = new LCD( Pins.GPIO_PIN_D11, // RS Pins.GPIO_PIN_D9, // Enable Pins.GPIO_PIN_D7, // D4 Pins.GPIO_PIN_D5, // D5 Pins.GPIO_PIN_D3, // D6 Pins.GPIO_PIN_D1, // D7 20, // Number of Columns LCD.Operational.DoubleLIne, // LCD Row Format 4, // Number of Rows in LCD LCD.Operational.Dot5x8); // Dot Size of LCD lcd.ShowCursor = true; lcd.Show("www.Embedded-Lab.comWelcome's you to Netduino Tutorial site. Happy Learning! :)", 200, true); Thread.Sleep(1000); // reading time for the viewer |
As you can see we created an instance of LCD class and then set some properties to what we like and simply called the Show method. There are two Show methods, one will display the given text all at once and the other Show method will display one letter at a time.
Now let’s dig into the complex part. There are several libraries out there but I wrote my own to understand what’s cooking inside. Let’s look at the constructor section,
public LCD(Cpu.Pin rs, Cpu.Pin enable, Cpu.Pin d4, Cpu.Pin d5, Cpu.Pin d6, Cpu.Pin d7, byte columns, Operational lineSize, int numberOfRows, Operational dotSize) { RS = new OutputPort(rs, false); Enable = new OutputPort(enable, false); D4 = new OutputPort(d4, false); D5 = new OutputPort(d5, false); D6 = new OutputPort(d6, false); D7 = new OutputPort(d7, false); Columns = columns; DotSize = (byte)dotSize; NumberOfLines = (byte)lineSize; NumberOfRows = numberOfRows; Initialize(); } |
In the constructor section, it basically creates some Outport, saves the LCD properties and then calls the Initialize method. In this method, we set visual properties, initialize some arrays and then prepare the LCD for 4 bit communication mode.
private void Initialize() { //initialize fields isVisible = true; showCursor = false; isBlinking = false; rowAddress = new byte[] { 0x00, 0x40, 0x14, 0x54 }; firstHalfAddress = new byte[] { 0x10, 0x20, 0x40, 0x80 }; secondHalfAddress = new byte[] { 0x01, 0x02, 0x04, 0x08 }; currentRow = 0; dirtyColumns = 0; Thread.Sleep(50); // must wait for a few milliseconds // RS to high = data transfer // RS to low = command/instruction transfer RS.Write(false); // Enable provides a clock function to synchronize data transfer Enable.Write(false); // Set for 4 bit model Write(0x03, secondHalfAddress); Thread.Sleep(4); Write(0x03, secondHalfAddress); Thread.Sleep(4); Write(0x03, secondHalfAddress); Thread.Sleep(150); Write(0x02, secondHalfAddress); // Set the LCD properties byte operationalValue = (byte)((byte)Operational.FourBit | (byte)NumberOfLines | (byte)DotSize); SendCommand((byte)((byte)Command.Operational | operationalValue)); UpdateDisplayOptions(); ClearDisplay(); byte entranceValue = (byte)Entrance.FromLeft | (byte)Entrance.ShiftDecrement; SendCommand((byte)((byte)Command.Entrance | entranceValue)); } |
Now, let’s look at the methods that are critical to show the text to the LCD. The first Show method allows us to show the given text letter by letter as you can see the loop is structured for each character in the given text.
public void Show(string text, int delay, bool newLine) { if (newLine) dirtyColumns = 0; foreach (char textChar in text.ToCharArray()) { ResetLines(); Show(Encoding.UTF8.GetBytes(textChar.ToString())); dirtyColumns += 1; Thread.Sleep(delay); } } |
The second Show method basically shows the whole text at once but before that it does some formatting so that the text will appear continuously. Trust me showing given text in a continuous way is one of the difficult part that I resolved in this LCD class.
public void Show(string text) { string[] splitedText = SplitText(text); Show(splitedText); } |
Finally, the method that writes information to the LCD is done under Write method. The first Write method calls the send Write method it passes the write value and the address where to send the information. The second Write method basically writes the information to the LCD.
private void Write(byte[] data) { foreach (byte value in data) { Write(value, firstHalfAddress); // First half Write(value, secondHalfAddress); // Second half } } private void Write(byte value, byte[] halfAddress) { D4.Write((value & halfAddress[0]) > 0); D5.Write((value & halfAddress[1]) > 0); D6.Write((value & halfAddress[2]) > 0); D7.Write((value & halfAddress[3]) > 0); Enable.Write(true); Enable.Write(false); //Debug.Print("Wrote " + value.ToString()); } |
Output
After connecting a few wires, when you run your code and visualize the text that you wanted, puts smile in your face. Depending upon which Show method you are using will give you get different results, one will show letter by letter and other will show whole text at once. As in the video, when you rotate the potentiometer, the display contrast changes.
A small Video based on the following code:
lcd.ShowCursor = true; lcd.Show("www.Embedded-Lab.comWelcome's you to Netduino Tutorial site. Happy Learning! :)", 200, true); Thread.Sleep(1000); // reading time for the viewer lcd.ClearDisplay(); lcd.Show("That was cool! Let's clear the display and show all text at once", 200, true); Thread.Sleep(1000); // reading time for the viewer lcd.ClearDisplay(); lcd.ShowCursor = false; lcd.Show("ABCDEFGHILKLMnopqrstuvwxyz0123456789 -Thanks!"); |
Downloads
1) C#.NET Code (Solution file)
What Next
In our next tutorial we will learn about interfacing seven segments LED displays to Netduino. Seven segments LEDs commonly found in many electronics equipments as front panel displays. The next tutorial will also include a Light Dependent Resistor (LDR) to sense the surrounding light intensity that will be displayed on 4 seven segment LEDs.
|
|




Pingback: Manejo de pantallas LCD con Netduino « Soloelectronicos
Pingback: Tutorial Netduino parte2 « Soloelectronicos
hello,i have tried running that code but havent been successful.is there a way you could help me?you could show me how the entire program flows in microsoft visual studio.
thanks
Pingback: Blog J.Schweiss | AVR Tutorials
Pingback: Netduino and LCD interfacing tutorial | ?PCB??
Pingback: Embedded Labs: LCD and Netduino Plus | Controller Freak